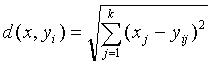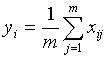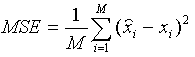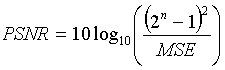Vector Quantization
This page contains information related
to
vector quantization (VQ). Currently this page includes information
about VQ with regards to compression. In the future, we will make this
page a more comprehensive VQ page.
In what applications is VQ used?
Vector quantization is used in many
applications such as image and voice compression, voice recognition (in
general statistical pattern recognition), and surprisingly enough in volume
rendering (I have no idea how VQ is used in volume rendering!).
What is VQ?
A vector quantizer maps k-dimensional
vectors in the vector space Rk
into a finite set of vectors
Y = {yi:
i
= 1, 2, ..., N}. Each vector yi
is called a code vector or a codeword.
and the set of all the codewords is called a codebook. Associated
with each codeword, yi,
is a nearest neighbor region called Voronoi region, and it is defined
by:
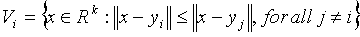
The set of Voronoi regions partition
the entire space Rk
such that:
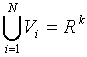
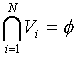 for all
i
for all
i j
j
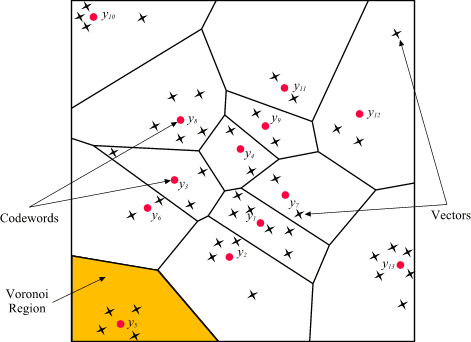
As an example we take vectors in
the two dimensional case without loss of generality. Figure 1 shows
some vectors in space. Associated with each cluster of vectors is
a representative codeword. Each codeword resides in its own Voronoi
region. These regions are separated with imaginary lines in figure
1 for illustration. Given an input vector, the codeword that is chosen
to represent it is the one in the same Voronoi region.
|
| Figure 1: Codewords in 2-dimensional
space. Input vectors are marked with an x, codewords are marked with
red circles, and the Voronoi regions are separated with boundary lines. |
The representative codeword is determined
to be the closest in Euclidean distance from the input vector. The
Euclidean distance is defined by:
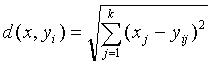
where xj
is the jth component of the input vector, and yij
is the jth is component of the codeword yi.
How does VQ work in compression?
A vector quantizer is composed of two
operations. The first is the encoder, and the second is the decoder.
The encoder takes an input vector and outputs the index of the codeword
that offers the lowest distortion. In this case the lowest distortion
is found by evaluating the Euclidean distance between the input vector
and each codeword in the codebook. Once the closest codeword is found,
the index of that codeword is sent through a channel (the channel could
be a computer storage, communications channel, and so on). When the
encoder receives the index of the codeword, it replaces the index with
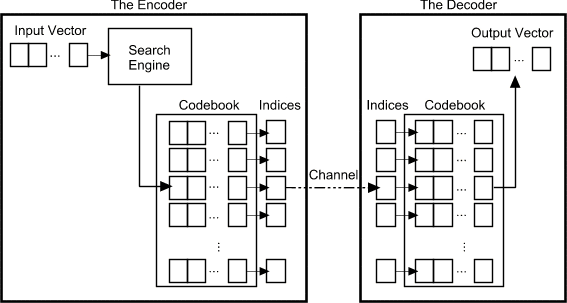
the associated codeword. Figure 2 shows a block diagram of the operation
of the encoder and decoder.
|
| Figure 2: The Encoder and decoder
in a vector quantizer. Given an input vector, the closest codeword
is found and the index of the codeword is sent through the channel.
The decoder receives the index of the codeword, and outputs the codeword. |
How is the codebook designed?
So far we have talked about the way
VQ works, but we haven't talked about how to generate the codebook.
What code words best represent a given set of input vectors? How
many should be chosen?
Unfortunately, designing a codebook
that best represents the set of input vectors is NP-hard. That means
that it requires an exhaustive search for the best possible codewords in
space, and the search increases exponentially as the number of codewords
increases (if you can find an optimal solution in polynomial time your
name will go down in history forever). We therefore resort to suboptimal
codebook design schemes, and the first one that comes to mind is the simplest.
It is named LBG
for Linde-Buzo-Gray, the authors of this idea. This algorithm is
similar to the k-means algorithm.
The algorithm
-
Determine the number of codewords,
N,
or the size of the codebook.
-
Select N codewords at random,
and let that be the initial codebook.
The initial codewords can be randomly chosen from the set of input vectors.
-
Using the Euclidean distance measure
clusterize the vectors around each codeword.
This is done by taking each input vector and finding the Euclidean distance
between it and each codeword. The input vector belongs to the cluster
of the codeword that yields the minimum distance.
-
Compute the new set of codewords.
This is done by obtaining the average of each cluster. Add the component
of each vector and divide by the number of vectors in the cluster.
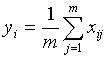
where i is the component
of each vector (x, y, z, ... directions), m is the number of vectors
in the cluster.
-
Repeat steps 2 and 3 until the either
the codewords don't change or the change in the codewords is small.
This algorithm is by far the
most popular, and that is due to its simplicity. Although it is locally
optimal, yet it is very slow. The reason it is slow is because for
each iteration, determining each cluster requires that each input vector
be compared with all the codewords in the codebook (We have programmed
this algorithm in C, and for an 512x512 image, a codebook of 256, and vectors
in 4 dimensions, the generation of the codebook took about 20 minutes on
an HP machine).
There are many other methods to designing
the codebook, methods such as Pairwise
Nearest Neighbor (PNN),
Simulated Annealing, Maximum Descent (MD), and Frequency-Sensitive
Competitive Learning (FSCL),
etc.
How does the search engine work?
Although VQ offers more compression
for the same distortion rate as scalar quantization and PCM, yet is not
as widely implemented. This due to two things. The first is
the time it takes to generate the codebook, and second is the speed of
the search. Many
algorithms have be proposed to increase the speed of the search.
Some of them reduce the math used to determine the codeword that offers
the minimum distortion, other algorithms preprocess the codewords and exploit
underlying structure.
The simplest search method, which
is also the slowest, is full search. In full search an input vector
is compared with every codeword in the codebook. If there were M
input vectors, N codewords, and each vector is in k dimensions,
then the number of multiplies becomes kMN, the number of additions
and subtractions become MN((k - 1) + k) = MN(2k-1),
and the number of comparisons becomes MN(k - 1). This
makes full search an expensive method.
What is the measure of performance VQ?
How does one rate the performance of
a compressed image or sound using VQ? There is no good way to measure
the performance of VQ. This is because the distortion that VQ incurs
will be evaluated by us humans and that is a subjective measure.
Don't despair! We can always resort to good old Mean Squared Error
(MSE) and Peak Signal to Noise Ratio (PSNR). MSE is defined
as follows:
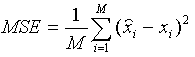
where M is the number of elements
in the signal, or image. For example, if we wanted to find the MSE
between the reconstructed and the original image, then we would take the
difference between the two images pixel by pixel, square the results, and
average the results.
The PSNR is defined as follows:
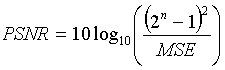
where n is the number of bits
per symbol. As an example, if we want to find the PSNR between two
256 gray level images, then we set n to 8 bits.
Some sites with VQ
Although there are many web pages on
VQ, but the majority of them are not generalized. The majority of
these sites describe new ways of implementing VQ or some of its applications.
Unfortunately, most of these sites don't go into the detail of their work.
I have therefore limited the links to those sites that contain useful information
or tools.
VQers
This is a list of people, in alphabetical
order by last name, who constantly work on VQ. I call them
VQers.
They are a must know! If you think you are VQer, then send me an
email,
and I will include your name in the list.
You can email me at mohamedqasem@yahoo.com
if you have any questions or comments.
back
to my home page
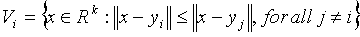
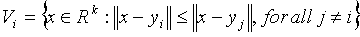
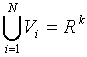
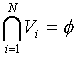 for all
i
for all
i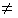 j
j